一、AB测试是什么?
AB测试即基于统计学原理, 通过合理流量分配, 高效、准确选取局部指标价值最大化方案的一系列方法论的总和.
二、为什么要用AB测试来评价方案的好坏?
商业社会, 由于功能设计者个人思维的局限性以及全量用户的不可调研性, 导致了一个功能的预期效果可能与实际上线后的效果存在认知、实用上的差异.
为了达到局部ROI最大化的目标(通常这一目标在潜在意义上会使得产品核心目标得以提升), 就需要用户自己“用脚投票”, 通过实际数据反馈来选出ROI最大化的功能方案.
基于这一商业目的, 多数互联网公司会采取AB测试来寻找能够为圈定指标带来最大收益的功能方案.
三、AB测试是如何“科学”选取高ROI方案的?
从本质上来看, 通常有两类方法可以判断一个方案的优劣好坏, 即定性分析与定量分析.
其中定性分析由于过于主观, 非常考验一个分析者自身的思维能力, 且容易陷入思维误区, 得出实际错误却能说服自己的观点.
而真实世界中事件发生本质上是概率发生, 因此在较短时间内的定量指标对比, 也往往会因为事件本身波动而得出错误答案.
因此, 就需要寻找一套方法论, 即统计学. 以确保对功能方案评价不落入主观陷阱, 也不因特定事件波动而得出错误答案.
3.1 为什么使用统计学得出的结果是科学的?
原因有三.
其一, 互联网的功能方案往往是基于对用户行为的判断设计的, 而用户行为本质上就是一种行为概率. 点击或者不点击, 留存或者离开, 从模型上来讲, 就是一个典型的二项分布.
那么对于一个本质上是概率分布的事件行为来说, 最高效、科学的方法即使用假设检验/方差分析来从统计学意义上判断方案的优劣.
二项分布[1]: 在n次独立重复的伯努利试验中, 设每次试验中事件A发生的概率为p. 用X表示n重伯努利试验中事件A发生的次数, 则X的可能取值为0, 1, ..., n, 且对每一个k , 事件 即为"n次试验中事件A恰好发生k次", 随机变量X的离散概率分布即为二项分布(Binomial Distribution)
伯努利试验[2]: 伯努利试验(Bernoulli experiment)是在同样的条件下重复地、相互独立地进行的一种随机试验, 其特点是该随机试验只有两种可能结果: 发生或者不发生. 我们假设该项试验独立重复进行了n次, 那么就称这一系列重复独立的随机试验为n重伯努利试验, 或成为伯努利概型.
其二, 虽然假设检验也仅仅是从置信区间角度来判断方案优劣, 在一定条件下也是存在误判, 即发生第一类/第二类检验错误.
但这种方法是所有方法中最科学、有理论依据的. 当我们无法找到最有判断方法论时, 次优方法论往往就是最优方法论.
其三, 现实社会往往没有必要得出最准确的数值. 日活50.7万和日活52万其实是没有本质差别的. 概率意义上正确往往已经可以得出最接近真实的答案的.
四、AB测试的业务目的与流程
在阐述完AB测试的一些理论与现实背景后, 让我们来回到实际业务层面来了解AB测试.
4.1 目的
一般来讲, AB测试通常有可以划分为两大目的:
- 判断方案的优劣: 究竟是A方案好些, 还是B方案好些.
- 计算方案带来的ROI: 最近上了一个帖子功能, 究竟给平台带来了多数DAU, 多数额外使用时长.
4.2 通用流程方法论
AB测试,本质上就是把平台的流量均匀分为几组,在每一组添加不同的策略,基于预期的用户数据指标(如: 日活, 用户使用时长等)在统计学意义上的显著性水平, 选择一个最好的组上线。
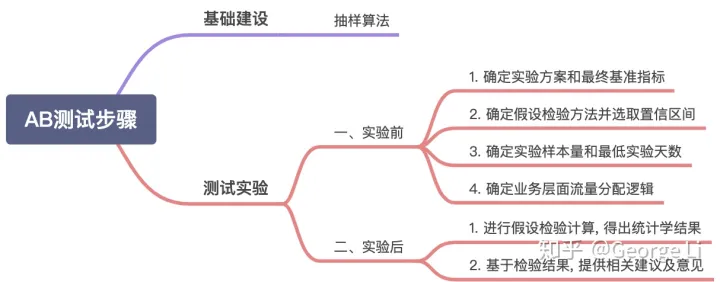
4.2.1 抽样算法
一个抽样算法的好坏, 往往就决定了这次AB测试的科学程度. 互联网公司最基础的抽样算法是对用户ID进行哈希取模后随机分组, 但这就有可能将高转化率的用户都分配至某一组,导致样本分组从源头即不可信.
因此需要在最开始就采用较为合理的抽样算法.
抽样算法是AB测试的基础, 后续会开单章详细阐述. 这文仅做介绍性阐述.
举个最简单的例子.
现在只有两个用户, 其中用户A注册后就流失了, 用户B在平台买了价值上万的商品, 我们通过哈希分组后, B所在组的人均购买一定是远远高于A的.
4.2.2 测试实验
1. 确定实验方案和最终基准指标
AB测试的开始, 一定是要先选择需上线的待测试方案的.
当方案选定之后, 就需要来确定最终基准指标了, 即为什么要改相关功能方案? 这对整个产品会带来哪些核心指标的改善? 是提升DAU还是提升转化率?
实验一定是有目的的,没有目的的实验是没有价值的.
2. 确定假设检验方法并选取置信区间.
在选取好最终基准指标之后, 就需要选择对应的假设检验方法了. 这边先给出一个简易、基于最终基准指标的假设检验选取方法论.
- 均值型指标: 如人均时长, 人均购买
- 样本量很大时: z检验
- 样本量很小时: t检验
- 比值型指标: 如注册转化率、购买转化率
- 卡方检验.
假设检验方法内容较多, 后续会开单章详细阐述. 置信区间也会在其中提及. 通常取95%的置信区间.
3. 确定实验样本量和最低实验天数
要使得假设检验在统计学意义上是有意义的, 就需要该次实验的样本量达到理论上的最少样本量.
因此在设计实验时, 就需要计算出该次实验的最少样本量, 从而结合产品DAU推算出最少实验天数.
样本量选取原理较为复杂, 后续会开单章详细阐述.
4. 确定业务层面流量分配逻辑[3]
AB测试的背景通用有以下几种:
- 尽快得到实验结论并辅助决策
- 用户体验影响降至最小
因此经常需要在流量分配时有所权衡,一般有以下几个情况:
- 不影响用户体验:如 UI 实验、文案类实验等,一般可以均匀分配流量实验,可以快速得到实验结论
- 不确定性较强的实验:如产品新功能上线,一般需小流量实验,尽量减小用户体验影响,在允许的时间内得到结论
- 希望收益最大化的实验:如运营活动等,尽可能将效果最大化,一般需要大流量实验,留出小部分对照组用于评估 ROI
5. AB测试实验效果评估[3]
5.1 判断AB测试实验优劣
这块较为简单, 对相关指标进行假设检验, 判断在一定置信区间水平下的显著性水平即可.
5.2 计算方案的ROI
ROI即投资回报比.
通常情况下, 方案的成本是可以直接计算的; 而对于收益而言, 就需要计算与对照组的差值来得出来.
我们假定以总日活跃天(即DAU按日累计求和)作为收益指标, 需要假设不做运营活动, DAU会是多少, 可以通过对照组进行计算, 即:
- 日活跃天(实验组假设不做活动) = 对照组日活跃天 * (实验组流量 / 对照组流量)
- 收益(实验组) = 日活跃天(实验组做活动) - 日活跃天(实验组假设不做活动)
五、AB测试注意事项[3]
5.1 新鲜劲数据陷阱
用户对于产品中的新功能往往会产生好奇, 而这一好奇在数据层面就会反映在点击上.
因此在做AB测试评估时, 需要观测指标到稳定态后, 再做评估.
避免新鲜劲数据陷阱.
5.2 人群差异陷阱
由于不同人群在指标上先天存在差异, 因此在分析AB测试结果时, 需要考虑到不同人群的差异.
这也是抽样算法合理性的意义所在. 一个较为科学合理的抽样算法, 能在很大程度上规避掉不同人均的影响差异, 做到基于基准指标的分层随机抽样. 确保基准指标的分布基本一致.
新用户的使用时长往往会比老用户低很多, 比会员用户低更多.
最近在理自己的数据分析底层逻辑. 因此会定期输出对于数据分析的宏观理解和专项体系阐述.
其中AB测试算是数据分析师进阶的底层能力之一吧, 因此大概会出4-5篇相关的文章进行阐述.
当然在阐述中也会借鉴一些答主回答和大公司玩法, 如有相关借鉴都会列入参考文献中.
这篇算是AB测试的开山之篇, 除了自身对于AB测试的理解之外, 不少观点和想法借鉴了腾讯技术工程在"什么是A/B测试"下的回答. 特别是对于ROI的计算, 真的受益匪浅.

