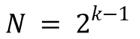编译:Zoe Zuo、张南星、元元、Aileen
量子纠缠这两天忽然火了,还是因为一件与科技互联网都完全无关的桃色事件。
没有看懂的同学可自行搜索。
被爱因斯坦称为“幽灵般的超距作用”的量子纠缠,有没有可能发生在两个人类个体身上?量子计算到底有什么神奇之处?
虽然人类历史上的技术革新几经波澜壮阔,依然有一些计算问题在数字革命中遗存下来,似乎无法被攻克。受到这些问题的掣肘,科技上的关键性突破迟迟不能实现,甚至全球经济也为此拖累。
在过去的几十年里,传统计算机的计算能力和处理速度几乎每两年就翻番,但似乎在解决这些一直存在的计算问题上毫无进展。
想知道为什么吗?你去询问任何一个计算机科学家,他们大概都会给出这样的答案:目前的传统数字计算机都是建立在一个局限性颇多的传统计算模型上的。放眼长远,要高效地解决世界上那些最根深蒂固的计算问题,我们必须诉诸一个全新的、更为强大的家伙:量子计算机。
从根本上说,传统计算机和量子计算机之间的差别并非是一辆旧车和一辆新车的差别,而是一匹马和一只鹰的差别:前者虽然能跑,但是后者会飞。两种计算机就是如此迥然不同。在这里,我们要仔细看看关键性差异具体体现在何处,深入理解究竟是什么让量子计算机如此出类拔萃。本文不会告诉你量子计算机最根本的工作原理,因为没有人真的知道答案。
一、传统计算机的硬限制
1. 摩尔定律
近几十年来,传统计算机的运行速度与计算能力每两年就翻倍(另一说仅18个月),这就是著名的摩尔定律(Moore's law)。尽管这种惊人的更新速度已经开始放缓,但我们多少可以相信,今天体型庞大的超级计算机会进化成明天物美价廉的笔记本电脑。依照这种发展速度,我们也有理由假定,在可预见的未来,没有什么计算任务是传统计算机完成不了的。然而,除非我们所说的未来是指万亿年之后(或者更久),否则我们的假定对于某些棘手的计算任务来说完全不可靠。
2. 传统计算机的致命弱点
事实上,诸如算出大整数的质因数这样的计算任务,即使是未来速度最快的传统计算机也无法完成。背后的原因在于,计算一个数的质因数的复杂度呈指数式增长。什么是指数式增长(exponential growth)?我们得探究一下这个概念,因为这对于我们理解为什么量子计算机潜力巨大而传统计算机后劲不足至关重要。
3. 指数增长
有些事物是按照固定速度增长的,有些事物则随着总数量的增加而增长得越来越快。当增长的速度随着总量逐渐增加而变得更快(而非恒定)时,这一增长就是指数式的。
指数式增长是极其强大的,它最重要的特征之一就是,起初增长缓慢,而后以惊人的方式迅速增长到巨大的总量。
不举例子的话,这个定义可能有点难以捉摸,所以让我们先看个小故事吧。
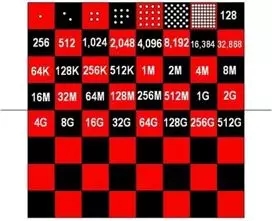
传说有个国王答应奖励一个聪明人,这个人便向国王请求奖励他大米,规则是在棋盘的第一个格子上放一粒米,第二个格子上放两粒米,第三个格子上放四粒米,然后以此类推,每一个格子上的米粒数须是前一个格子上的二倍。国王欣然应允,但很快就意识到,要填满整个棋盘,所需的大米数量远远多于全国大米存量,而且会花掉他所有的财产。
米粒的指数式增长
任何一个方格上的米粒数量都符合以下规则,或者说公式:
在这个公式里,k指方格的序号,N指该方格上米粒的数量。
- 如果k=1(第一个方格),那么N = 2⁰,等于1。
- 如果k=5(第五个方格),那么N = 24,等于16。
这就是指数型增长,因为这里的指数或者说幂是随着方格的推移而增加的。
为了更进一步解释这个概念,我作了图来表示一个指数型函数是如何随着输入量的增加而增长的。
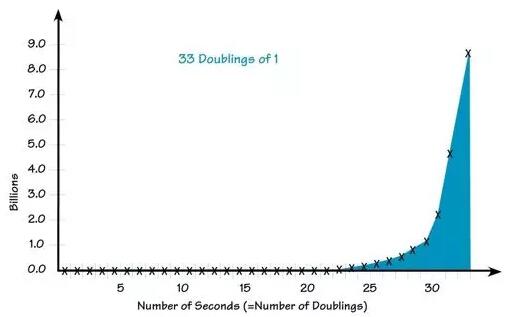
1的33次倍增
X坐标轴:秒数(=倍增次数),Y坐标轴:百万
由图可知,该函数开始时增长相对缓慢,但没多久就急剧增长到传统计算机在没有足够输入规模的情况下无法计算出来的数字。
4. 指数增长函数造成的结果
好了,故事就讲到这里,我们将目光转向现实世界中的指数问题,比如我们之前提到的那个问题:质因数分解(prime factorization)。
以数字51为例,看看你多久能找到两个不同的质数,使得这两数乘积为51。如果你熟悉这类问题的话,大概只需要几秒钟就能想出答案,3和17这两个质数相乘可得51。
事实证明,这样看似简单的过程却是数字经济的核心,是最安全的加密算法的基础。我们之所以在加密中采用这一技术,是因为质因数分解中涉及的数字会越来越大,导致传统计算机越来越难以分解它们。当数字位数达到一定规模,即使用速度最快的传统计算机进行分解,也要花费数月、数年、数个世纪、数千年,乃至永远。
考虑到这点,传统计算机就算在可预见的未来能够持续实现运算能力每两年翻番(当然这不大可能),也永远无法彻底解决质因数分解的问题。现代科学和数学的一些核心问题同样棘手,包括分子模拟和数学上的最优化问题。任何试图深入这些问题的超级计算机定会以崩溃告终。
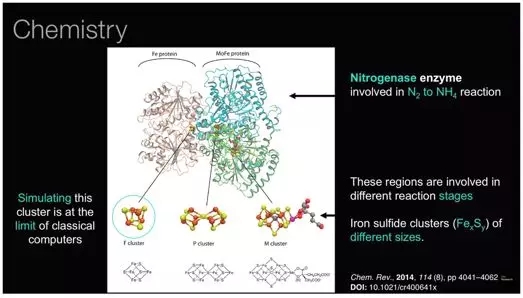
下面是来自IBM Research的一幅精彩插图,该图展示了世界上最强大的超级计算机所能模拟出的最复杂的分子F团簇(F cluster)。你能发现(在图片左下方),该分子其实根本不复杂,如果我们想借助模拟更为复杂的分子的方法来寻找更好的药物疗法、研究生物,我们就得另辟蹊径。
分子模拟问题
图注:
- Chemistry:化学
- Nitrogenase enzyme…:参与氮气(N2)转化为铵根(NH4)过程的固氮酶
- Simulating this cluster…:模拟该簇已经是传统计算机运算能力的上限
- These regions are…:这些区域参与了不同的反应阶段
- Iron sulfide clusters…:不同规模的铁硫簇(FexSy)
- Fe Protein:铁蛋白
- MoFe Protein:钼铁蛋白
- F cluster:F团簇
- P cluster:P团簇
- S cluster:S团簇
二、走进量子计算机
传统计算机在严格意义上是数码系统,纯粹依赖于传统计算原理与性质。量子计算机则是严格的量子系统,相应地依赖于量子的原理与性质,其中最重要的两点就是量子叠加(superposition)与量子纠缠(entanglement),它们赋予量子计算机非凡的能力,以解决那些看似无法克服的难题。
1. 量子叠加
要理解叠加的概念,我们先了解最简单的系统:双态系统(two-state system)。开/关转换(On/Off switch)就是一种普通、传统的双态系统,它总处于开或者关的状态。
一个双态量子系统(two-state quantum system)就完全是另一回事了。当然,无论你何时观测量子系统的状态,都会发现它确实处于开或者关的状态,但是在你没有观测时,一个量子系统是有可能处于开关同时存在的叠加状态的。无论有多么反直觉,甚至超自然,这种状态确实有可能出现。
量子叠加
一般而言,物理学家认为讨论量子系统在受观测之前的状态是没有意义的,比如自旋(spin)状态。有些人甚至认为,观测量子系统的行为会导致量子从不确定的模糊状态坍缩到你测量到的某种值(开或关,向上或向下)。虽然可能无法想象,但不能否认这种神秘的现象不仅真实存在,而且为提高解决问题的能力开辟出一个新维度,也为量子计算机奠定了基础。记住叠加的概念,我们稍后会介绍叠加是如何运用于量子计算的。
叠加存在的可能性不在本文的讨论范围内,但请相信它确实已经被证实了。如果你想要知道是叠加是如何产生的,你得先了解波粒二象性( Wave/Particle Duality)的概念。
2. 量子纠缠
那么我们继续谈谈建造量子计算机所用到的另一个量子原理:量子纠缠。
众所周知,一旦两个量子系统开始相互作用,它们就会不可救药的成为纠缠的伙伴。自此,无论两个系统相距多远,一个系统的状态可以准确反映另一个系统的状态。真的,两个系统之间即使相距几光年,它们仍旧能够及时准确的反映彼此的信息。
这个现象让爱因斯坦都觉得不可思议。(爱因斯坦对此有个著名的描述,“幽灵般的超距作用”)。我们借由一个实例来展示这个现象。
量子纠缠 (纠缠的量子比特的状态无法独立来看)
假设有两个电子A、B,一旦让它们以正确的方式相互作用,它们的旋转就会自动产生纠缠效应。自此,如果A向上旋转,那么B就会向下旋转,就像两个小孩在跷跷板两端一样。但是A和B即使在地球两端,亦或是在银河两端,也是这样。无论中间相隔上万英里、几光年,A、B的自旋相反已经被证实。但是需注意:这些系统的状态没有准确的取值,例如旋转的方向。它们在被测量之前以一种模糊叠加的方式存在。
所以在两个系统相隔几光年远的情况下,我们测量A的行为是否真的能导致B瞬间坍缩到相反的状态?如果确实如此,那么我们将面临另外一个问题:爱因斯坦告诉我们,在两个系统之间传递比如光信号这样的影响因素不可能超越光速。所以这个现象的根本原因是什么?老实说,我们真不知道。现在唯一已知的就是量子纠缠这个现象是真实存在的,而人类可以利用它创造奇迹。
3. 量子比特
量子计算中量子比特承担的任务就好比传统计算机中比特承担的任务:它是信息的基本单元。但是和量子比特币相比,比特就是彻头彻尾的无趣了。虽然在计算过程中,比特和量子比特都有两个状态(0或1),但是量子比特在计算结束之前能够同时处于0或者1的状态。这听起来有点像量子叠加对吗?这确实就是量子叠加。量子比特是量子系统中最突出的一个存在。
经典比特,量子比特
就像传统计算机建立在一个个比特、开或关的晶体管之上,量子计算机建立在一个个量子比特、上/下旋转的电子之上(如果能够观测到的话)。同样的,串联起来的开、关晶体管形成了逻辑闸,以供数字计算机进行传统方法的运算;而处于上/下旋转状态的电子串联起来,则形成了量子闸以供量子计算机进行量子运算。然而,要把单个电子串联起来(还有保持它们的旋转状态),做起来远比说起来难。
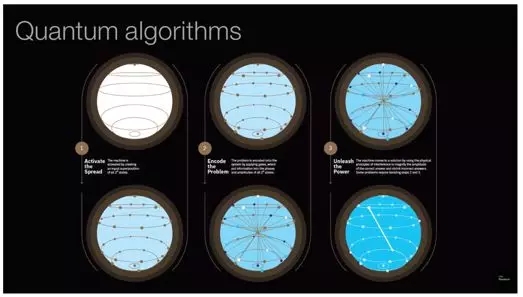
量子算法
图注:
- 激发电子分化(通过创建2^n个状态的平等叠加态来激活机器)
- 问题编码(利用逻辑闸给问题编码,把信息写入2^n个状态的相和振幅中)
- 开启运算(通过物理干涉原理,机器放大正确答案的振幅,缩小错误答案的振幅,从而得到最终答案。有一些问题需要重复步骤2和3)
三、我们现在走到哪一步了?
在英特尔大量产出承载十多亿晶体管高度集成的传统芯片时,世界上最顶尖的实验计算机科学家还在努力把一小撮量子比特放到量子计算机的“芯片”上。为了体会出人类在量子计算这条路上还有多远的路要走,我们看一个例子:IBM最近发布了世界上最大的量子计算机,上面惊人地有……50个量子比特。
尽管如此,量子计算机已经启程,如果量子计算机的发展也遵循诸如摩尔定律之类的定理,那么我们很快就能发明出有好几百个、甚至是上千个量子比特的“芯片”。十亿个?让我深吸口气冷静一下。
但是请注意,量子计算机其实无需这么多量子比特就能够让传统计算机在某些关键领域上望尘莫及,例如质数分类,分子建模以及许多传统计算机无法解决的优化问题。
1. 展望2018
无论如何,就现状而言,几乎每一台量子计算机都是花费上百万美元,几乎疯狂的科学家们通力合作的大项目。一般只有像IBM这样大型IT公司的研发部门,或者像麻省理工这样大型研究型大学的实验物理学专业,才有足够的能力研究量子计算机。
它们需要在接近于绝对零度的超低温下工作(这个温度甚至低于外太空的温度),并且在过程中需要使用精确频率的微波来与计算机中的每个量子比特建立联系。不必说,这种方法难以规模化。但是想想最初传统计算机所用的真空管也不能规模化,我们不要对初代量子计算机太过苛刻。
2. 路漫漫其修远兮
之所以量子计算机无法形成主流,最大的一个原因就在于顶尖科学家、发明家们还在努力解决错误率高、量子比特少的问题。我们解决这两个问题之后,就可以迅速提高计算机的“量子容量”。这是IBM提出的术语,用来描述每台量子计算机能进行的有效计算量。
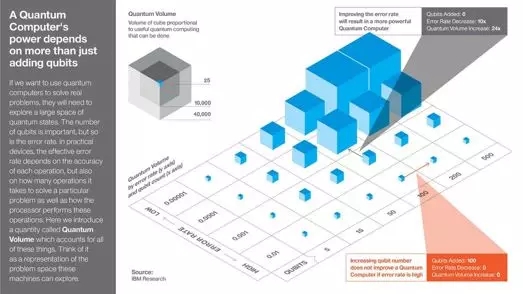
量子计算机的运算能力不只取决于增加量子比特数。量子容量,方块体积的大小与有效量子计算量成正比。
图注:
(1) 图中x坐标轴:量子比特(递增)
(2) 图中y坐标轴:误差率(递减)
(3) 图中灰色箭头:减少误差率可以提高量子计算机运算能力
- 量子比特增加: 0
- 误差率减少:10x
- 量子容量增加: 24x
(4) 图中红色箭头:在误差率高的情况下,提供量子比特数不能提高量子计算机运算能力
- 量子比特增加: 100
- 误差率减少:0
- 量子容量增加: 0
如果你想要用量子计算机来解决实际问题,它们需要在很大的量子状态空间中进行搜索。量子比特的数量很重要,误差率也同样重要。在实际设备中,误差率取决于每次操作正确与否,也取决于解决问题所需操作数量,以及处理器如何执行操作。这里我们提出“量子容量”这个数量术语,来整合上文提出的所有因素。可以将这个数量值视为代表机器可以有效搜索的问题域的大小。
简而言之,想要量子计算真正起飞、量子驱动的Macbook能够进入大众生活,我们需要更多的量子比特和更少的错误率。这需要一定的时间,但至少我们知道我们的目标,以及我们面临的障碍。
四、迷思还是解析
虽然量子计算机能够轻松完成传统计算机力不能及的事,但其实我们并不知道原理。如果这让你失望,想想我们确实发明了初代量子计算机,并且牢记这个词——“量子”。近一个世纪,人类已经利用量子力解决了许多问题,但我们确实不知道它们是如何做到的。
作为量子家族的一份子,量子计算同样扑朔迷离。《量子计算和量子信息》的作者Michael Nielsen 认为,任何试图解释量子计算的尝试都不可能成功。毕竟,如Nielsen所言,如果能够有一个直观的解释来描述量子计算机是如何工作的(即你能想象出来的),那么传统计算机也能模仿这个范式。但是如果传统计算机也能模仿的话,那么这个模型就无法真正准确地描述量子计算机,因为我们对量子计算机的义就是,量子计算机能做到传统计算机无法做到的事情。
根据Nielsen的解释,量子并行是目前最受欢迎的量子计算假说。由于以后你将会听到很多量子并行的故事,所以暂且就先简单了解一下。量子并行最基本的一个论点就是,不同与传统计算机,量子计算机能够同时读取所有计算出来的结果(在一个操作指令下),而数字计算机只能一个挨一个的读取。Nielsen 认为这部分解释大致合理。
然而,Nielsen极其反对后半段解释,即量子并行假说认为量子计算机能够在这所有的结果中选出最佳的一个。他坚持认为量子计算机在屏幕之下所做到的事情,和其他量子系统一样,是我们所不可能弄懂的。我们可以看到输入和输出,但是中间发生了什么永远将是谜团。
原文链接:
https://towardsdatascience.com/the-need-promise-and-reality-of-quantum-computing-4264ce15c6c0