数据结构是一种在计算机中组织和存储数据的专门方法,使我们可以更有效地对存储的数据执行操作。数据结构在计算机科学和软件工程领域有着广泛而多样的使用范围。
几乎所有已开发的程序或软件系统都在使用数据结构。此外,数据结构属于计算机科学和软件工程的基础知识。当涉及到软件工程面试问题时,这是一个关键话题。因此,作为开发人员,我们必须对数据结构有很好的了解。
在这篇文章中,我将简要解释每个程序员都必须了解的 8 种常用数据结构。
1、数组(Arrays)
数组是一种固定大小的结构,可以容纳相同数据类型的项。它可以是整数数组、浮点数数组、字符串数组甚至数组的数组(例如二维数组)。数组是有索引的,这意味着可以进行随机访问。
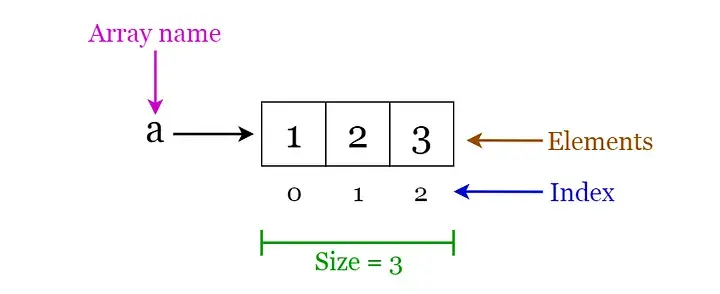
数组运算
- 遍历:遍历元素并打印它们。
- 搜索:搜索数组中的元素。您可以按元素的值或索引搜索元素
- 更新:更新给定索引处现有元素的值
由于数组的大小是固定的,因此无法立即向数组插入元素和从数组中删除元素。如果要将元素插入数组,首先必须创建一个大小增加的新数组(当前大小 + 1),复制现有元素并添加新元素。对于删除尺寸减小的新数组也是如此。
数组的应用
- 用作构建其他数据结构(例如数组列表、堆、哈希表、向量和矩阵)的构建块。
- 用于不同的排序算法,例如插入排序、快速排序、冒泡排序和合并排序。
2、链表(Linked Lists)
链表是一种顺序结构,由一系列按线性顺序相互链接的项目组成。因此,您必须顺序访问数据,而随机访问是不可能的。链接列表提供了动态集的简单而灵活的表示。
让我们考虑以下有关链表的术语。
- 链表中的元素称为节点。
- 每个节点都包含一个键和一个指向其后继节点(称为next )的指针。
- 名为head 的属性指向链表的第一个元素。
- 链表的最后一个元素称为尾部。

以下是可用的各种类型的链接列表。
- 单链表——项目的遍历只能向前进行。
- 双向链表——可以向前和向后两个方向遍历项目。节点由一个称为prev的附加指针组成,指向前一个节点。
- 循环链表——头部的prev指针指向尾部,尾部的next指针指向头部的链表。
链表操作
- 搜索:通过简单的线性搜索找到给定链表中第一个具有键k的元素,并返回指向该元素的指针
- 插入:向链表插入一个键。插入可以通过 3 种不同的方式完成;插入在列表的开头,插入在列表的末尾,插入在列表的中间。
- 删除:从给定的链表中删除元素x 。您无法通过一步删除节点。可以通过 3 种不同的方式进行删除;从列表开头删除、从列表末尾删除、从列表中间删除。
链表的应用
- 用于编译器设计中的符号表管理。
- 用于使用 Alt + Tab 在程序之间切换(使用循环链表实现)。
3、堆栈(Stacks)
堆栈是一种LIFO(后进先出 - 最后放置的元素可以首先访问)结构,在许多编程语言中都很常见。这种结构被命名为“堆栈”,因为它类似于现实世界中的堆栈——一堆盘子。
堆栈操作
下面给出了可以在堆栈上执行的 2 个基本操作。
- Push:将一个元素插入到栈顶。
- Pop:删除最上面的元素并返回。
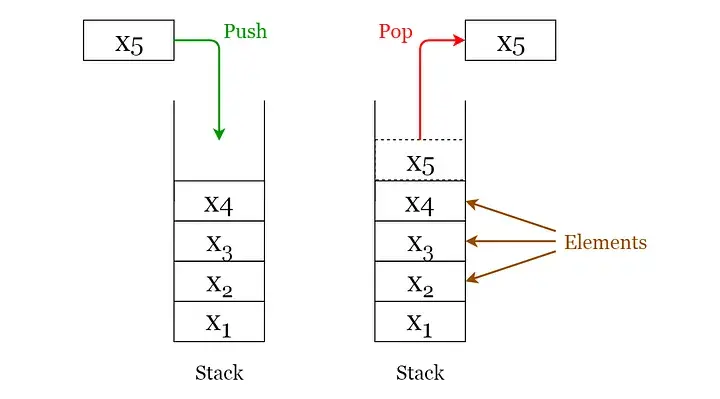
此外,还为堆栈提供了以下附加函数以检查其状态。
- Peek:返回栈顶元素而不删除它。
- isEmpty:检查堆栈是否为空。
- isFull:检查堆栈是否已满。
栈的应用
- 用于表达式求值(例如:用于解析和求值数学表达式的调车场算法)。
- 用于实现递归编程中的函数调用。
4、队列(Queues)
队列是一种FIFO(先进先出——先放置的元素可以先访问)结构,在许多编程语言中都很常见。这种结构被命名为“队列”,因为它类似于现实世界的队列——人们在队列中等待。
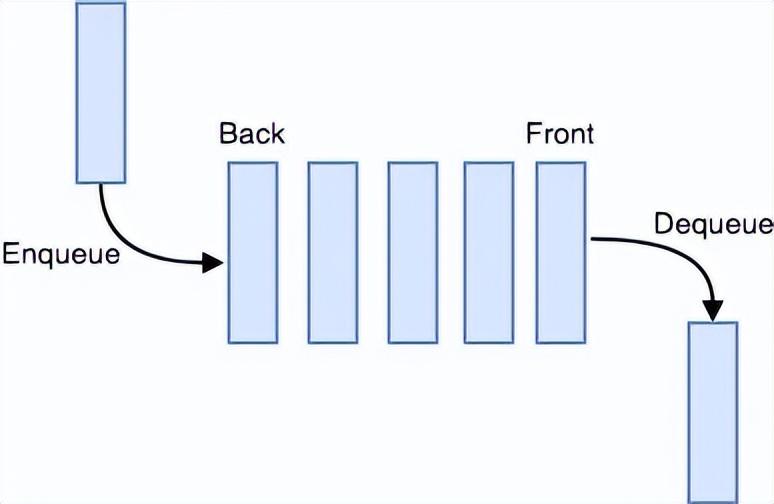
队列操作
下面给出了可以在队列上执行的 2 个基本操作。
- Enqueue:将一个元素插入到队列末尾。
- Dequeue:从队列开头删除元素。
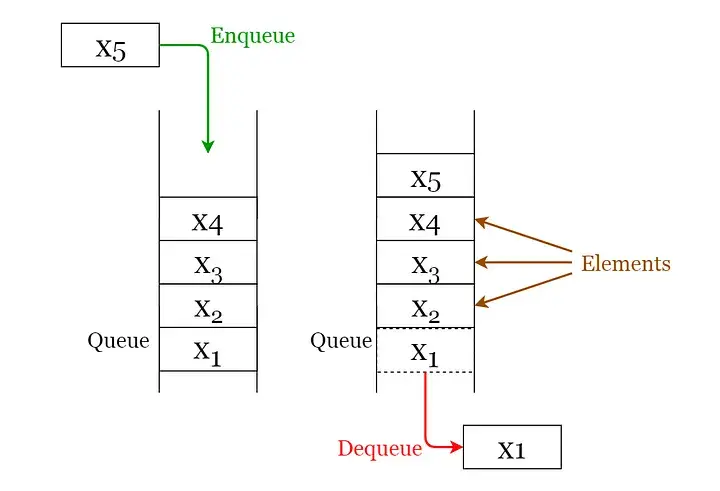
队列的应用
- 用于管理多线程中的线程。
- 用于实现排队系统(例如:优先级队列)。
5、哈希表(Hash Tables)
哈希表是一种存储值的数据结构,这些值具有与每个值关联的键。此外,如果我们知道与值关联的键,它就可以有效地支持查找。因此,无论数据大小如何,插入和搜索都非常有效。
直接寻址在表中存储时使用值和键之间的一对一映射。但是,当存在大量键值对时,这种方法会出现问题。该表将非常庞大,包含如此多的记录,并且考虑到典型计算机上的可用内存,可能不切实际甚至不可能进行存储。为了避免这个问题,我们使用哈希表。
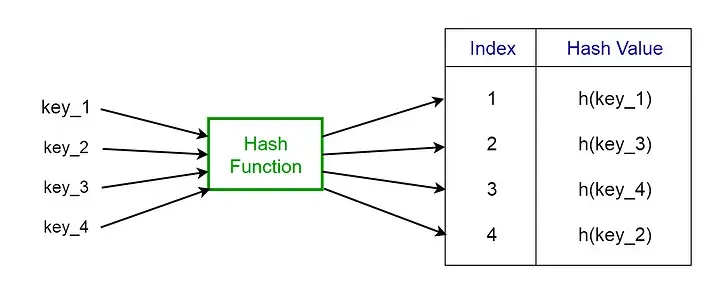
哈希函数
称为散列函数(h)的特殊函数用于克服直接寻址中的上述问题。
在直接访问中,具有键k的值存储在槽k中。使用哈希函数,我们计算每个值所在的表(槽)的索引。使用哈希函数对给定键计算出的值称为哈希值,它指示该值映射到的表的索引。
h(k) = k % m
- h:哈希函数。
- k:需要确定哈希值的Key。
- m:哈希表的大小(可用槽的数量)。对于m来说,不接近 2 的精确幂的素数是一个不错的选择。
考虑哈希函数h(k) = k % 20,其中哈希表的大小为 20。给定一组键,我们要计算每个键的哈希值,以确定它在哈希表中应位于的索引。考虑我们有以下键、哈希和哈希表索引。
- 1 → 1%20 → 1
- 5 → 5%20 → 5
- 23 → 23%20 → 3
- 63 → 63%20 → 3
从上面给出的最后两个示例中,我们可以看到,当哈希函数为多个键生成相同的索引时,可能会出现冲突。我们可以通过选择合适的哈希函数 h 并使用链接和开放寻址等技术来解决冲突。
哈希表的应用
- 用于实现数据库索引。
- 用于实现关联数组。
- 用于实现“集合”数据结构。
6、树(Trees)
树是一种层次结构,其中数据按层次结构组织并链接在一起。这种结构与链表不同,而在链表中,项目以线性顺序链接。
在程序的应用中,为了适应某些应用并满足某些限制,已经开发了各种类型的树木。一些例子是二叉搜索树、B树、treap、红黑树、splay树、AVL树和n叉树。
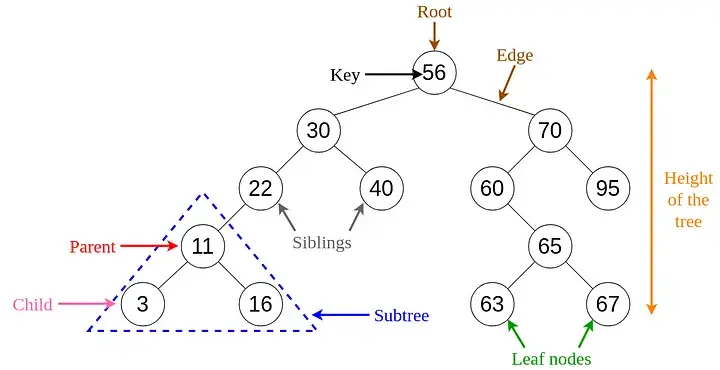
二叉搜索树
二叉搜索树(BST),顾名思义,是一种二叉树,其中数据以层次结构组织。该数据结构按排序顺序存储值。
二叉搜索树中的每个节点都包含以下属性。
- key:存储在节点中的值。
- left:指向左孩子的指针。
- right:指向右孩子的指针。
- p:指向父节点的指针。
二叉搜索树具有区别于其他树的独特属性。该属性称为二叉搜索树属性。
令x为二叉搜索树中的一个节点。
- 如果y是x左子树中的节点,则y.key ≤ x.key。
- 如果y是x右子树中的节点,则y.key ≥ x.key。
树的应用
- 二叉树:用于实现表达式解析器和表达式求解器。
- 二叉搜索树:用于许多数据不断进入和离开的搜索应用程序。
- 堆:JVM(Java 虚拟机)用来存储 Java 对象。
- Treaps:用于无线网络。
7、堆(Heaps)
堆是二叉树的一种特殊情况,其中父节点与其子节点的值进行比较,并进行相应的排列。
让我们看看如何表示堆。堆可以使用树和数组来表示。下面两张图显示了如何使用二叉树和数组来表示二叉堆。
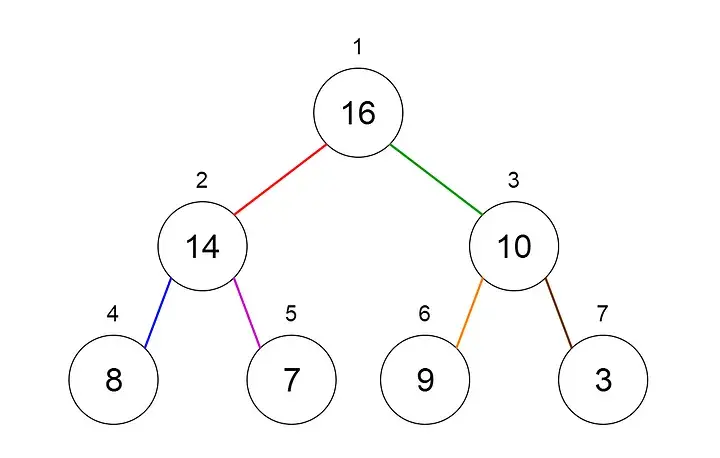
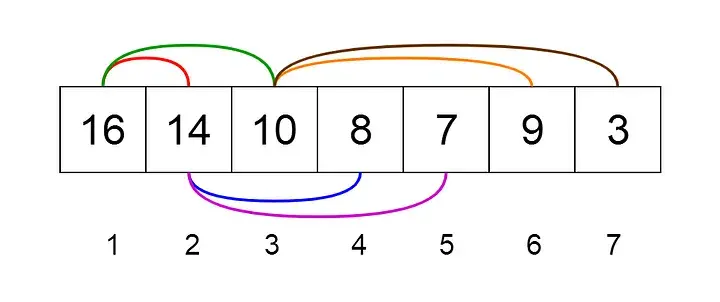
堆可以有两种类型
- 最小堆— 父级的键小于或等于其子级的键。这称为最小堆属性。根将包含堆的最小值。
- 最大堆— 父级的键大于或等于其子级的键。这称为最大堆属性。根将包含堆的最大值。
堆的应用
- 用于堆排序算法。
- 用于实现优先级队列,因为可以根据堆属性对优先级值进行排序,其中堆可以使用数组来实现。
- 队列函数可以在O(log n)时间内使用堆实现。
- 用于查找给定数组中 kᵗʰ 的最小(或最大)值。
8、图表(Graphs)
图由一组有限的顶点或节点以及一组连接这些顶点的边组成。
图的阶数是图中顶点的数量。图的大小是图中边的数量。
如果两个节点通过同一条边相互连接,则称它们是相邻的。
有向图
如果图G的所有边都具有指示起始顶点和终止顶点的方向,则称图 G 是有向图。
我们说(u, v)是从顶点u入射或离开顶点u ,并且是从顶点 v 入射或进入顶点v。
自循环:从顶点到自身的边。
无向图
如果图G的所有边都没有方向,则称其为无向图。它可以在两个顶点之间双向移动。
如果一个顶点没有连接到图中的任何其他节点,则称该顶点是孤立的。

图的应用
- 用于表示社交媒体网络。每个用户都是一个顶点,当用户连接时,他们会创建一条边。
- 用于表示搜索引擎的网页和链接。互联网上的网页通过超链接相互链接。每个页面是一个顶点,两个页面之间的超链接是一条边。用于百度中的页面排名。
- 用于表示 GPS 中的位置和路线。位置是顶点,连接位置的路线是边。用于计算两个位置之间的最短路线。
总结
还有很多种数据结构,其实都是基于以上数据结构变种生成的,数据结构是每个程序员都要掌握的,无论是工作中还是面试都必不可少的知识储备。

