一、是什么
排序是程序开发中非常常见的操作,对一组任意的数据元素经过排序操作后,就可以把他们变成一组一定规则排序的有序序列
排序算法属于算法中的一种,而且是覆盖范围极小的一种,彻底掌握排序算法对程序开发是有很大的帮助的
对于排序算法的好坏衡量,主要是从时间复杂度、空间复杂度、稳定性
时间复杂度、空间复杂度前面已经讲过,这里主要看看稳定性的定义
稳定性指的是假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变
即在原序列中,r[i] = r[j],且 r[i] 在 r[j] 之前,而在排序后的序列中,r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的
二、有哪些
常见的算法排序算法有:
- 冒泡排序
- 选择排序
- 插入排序
- 归并排序
- 快速排序
冒泡排序
一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来
思路如下:
- 比较相邻的元素,如果第一个比第二个大,就交换它们两个
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数
- 针对所有的元素重复以上的步骤,除了最后一个
- 重复上述步骤,直到没有任何一堆数字需要比较
选择排序
选择排序是一种简单直观的排序算法,它也是一种交换排序算法
无论什么数据进去都是 O(n2)的时间复杂度。所以用到它的时候,数据规模越小越好
唯一的好处是不占用额外的内存存储空间
思路如下:
在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕
插入排序
插入排序是一种简单直观的排序算法
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
解决思路如下:
- 把待排序的数组分成已排序和未排序两部分,初始的时候把第一个元素认为是已排好序的
- 从第二个元素开始,在已排好序的子数组中寻找到该元素合适的位置并插入该位置(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
- 重复上述过程直到最后一个元素被插入有序子数组中
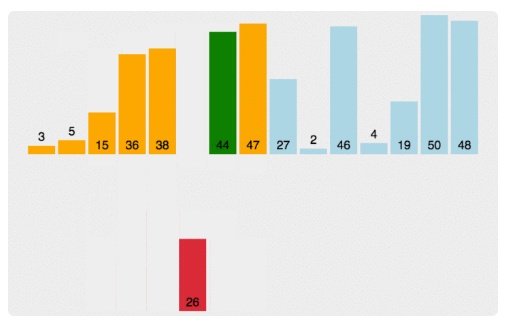
归并排序
归并排序是建立在归并操作上的一种有效的排序算法
该算法是采用分治法的一个非常典型的应用
将已有序的子序列合并,得到完全有序的序列,即先使每个子序列有序,再使子序列段间有序
解决思路如下:
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
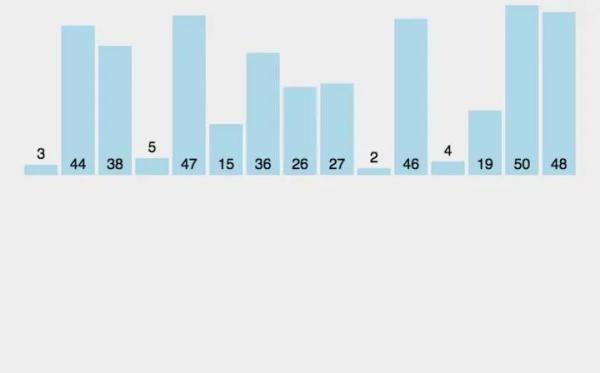
快速排序
快速排序是对冒泡排序算法的一种改进,基本思想是通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据比另一部分的所有数据要小
再按这种方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,使整个数据变成有序序列
解决思路如下:
- 从数列中挑出一个元素,称为"基准"(pivot)
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作
- 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序
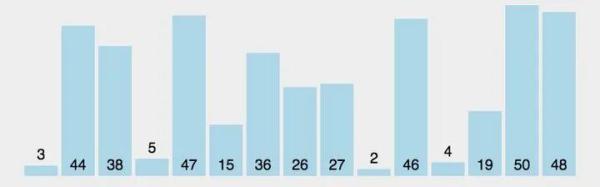
三、区别
除了上述的排序算法之外,还存在其他的排序算法,例如希尔排序、堆排序等等......
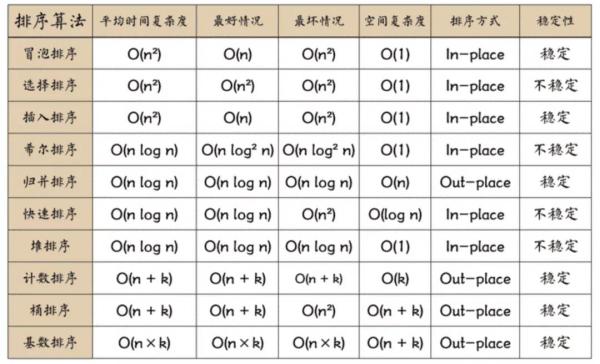
区别如下图所示:
参考文献
- https://www.runoob.com/w3cnote/bubble-sort.html
- http://www.x-lab.info/post/sort-algorithm/
- https://zhuanlan.zhihu.com/p/42586566